Prove them wrong #1 Testing the slope of a shower

Introduction

In this new series of my blog, I will explore real-life experiences through the lens of engineering principles. I'll begin with a TikTok video I saw where a construction engineer was testing the slope of a shower. He used a well-known method to determine that the slope was insufficient for proper drainage. His experiment was based on principles of physics and engineering, but some commenters disagreed with his findings. In this post, I'll demonstrate why those commenters were incorrect.

It is clear to see in the following video that the test failed, which led the engineer to refuse to accept the work and ask the worker to redo the ceramic again.

However, some comments disagree, but they are in Arabic, so let's prove them wrong.

Using the Lagrangian Method

Using the Lagrangian Method, I will solve the problem without delving deeply into the method's theoretical background. If necessary, I will explain the Lagrangian Method and prove the mechanics of solving the problem using different methods. For this demonstration, I will use the conservation of energy principle. Although real-life scenarios are not ideal, this approach will suffice to prove the point.

The Law of Conservation of Energy

Law Explanation:

Detailed explanation of the law:

Given that the object starts at rest from the top and has zero height at the bottom, and we neglect minor energy losses due to the shower surface being smooth, we arrive at this formula:

Applying the Lagrangian Method

Using the Lagrangian Method, which relies on the precise location of the object:

And PEx, depending on the current location of the ball:

And KEx:

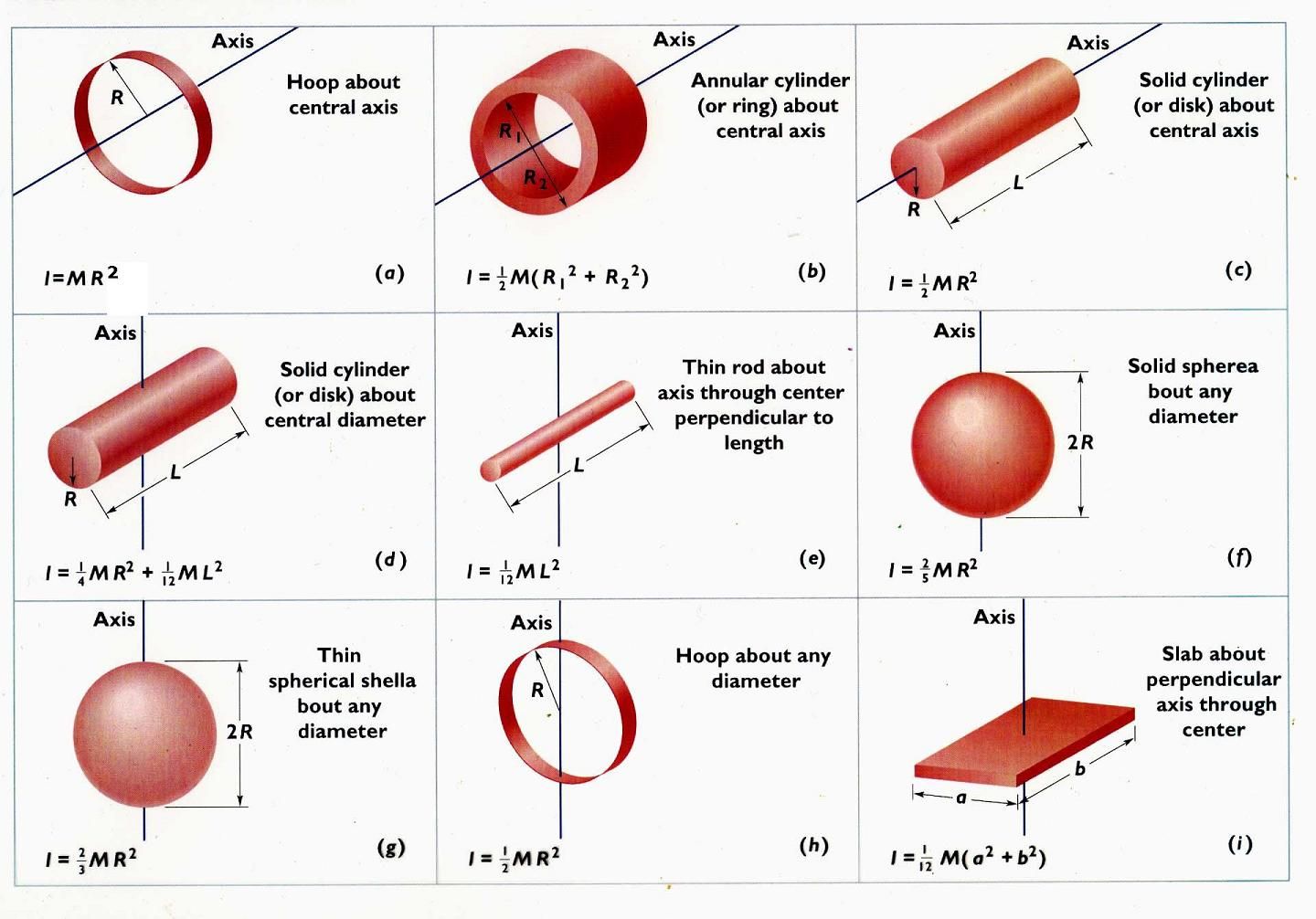
Since we are dealing with a solid cylinder, we can substitute the moment of inertia:

Solving the Differential Equation

Therefore:

where:

Finding the differential equation:

First, we take the partial derivative of the Lagrangian with respect to x dot:

Second, we take the derivative with respect to time:

Third, we take the partial derivative of the Lagrangian with respect to x:

Substituting all the formulas together:

Video demonstration

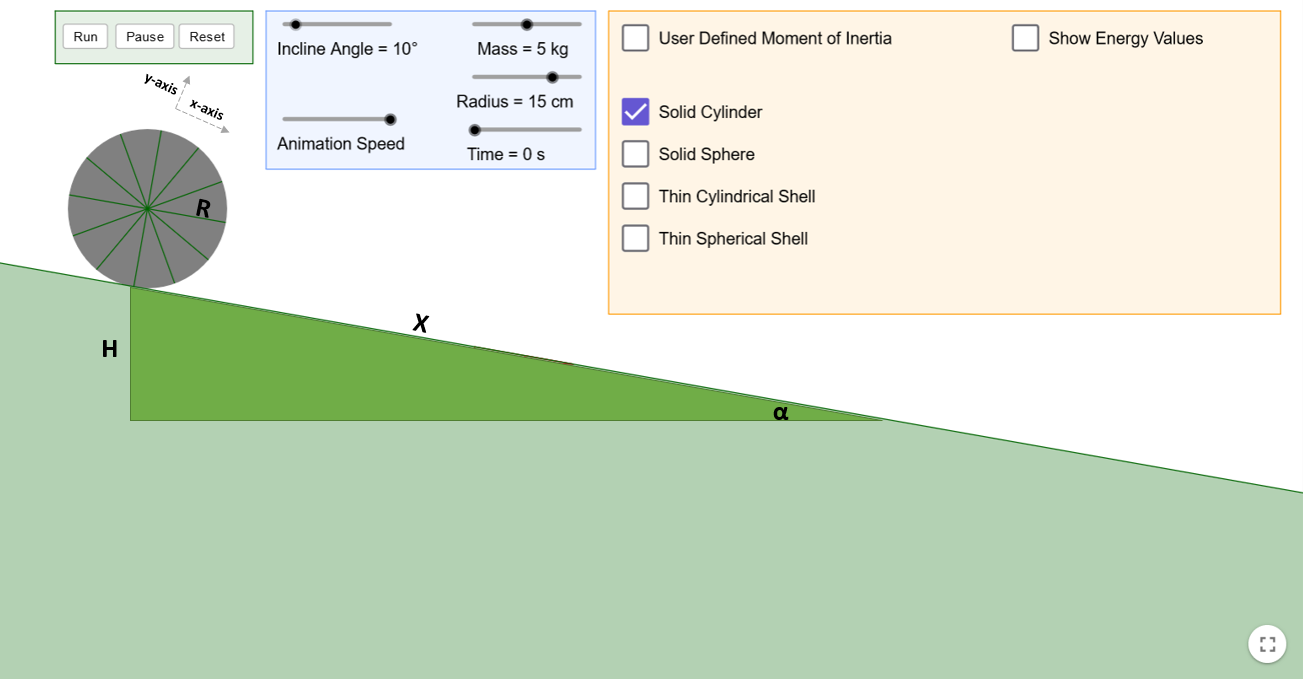
The following video demonstration shows variations in the radius and mass of the solid cylinder as well as the angle of the incline. The videos clearly show that the only significant factor affecting the rolling object is the angle of the incline. This conclusion might differ for objects that are not solid cylinders, such as solid spheres, but that is a different matter.

Mass: 5kg, angle: 10, radius:15cm

Mass: 10kg, angle: 10, radius:15cm

Mass: 1.5kg, angle: 10, radius:4cm

Mass: 5kg, angle: 1, radius:10cm

Conclusion

We found the acceleration of a rolling solid cylinder along an incline and observed that, both density (mass), and the radius of the object does not affect its velocity. This contradicts the comments in the video I shared, where people disagreed with the engineer's test. The angle in a practical setting is around 1.5-2.0 degrees, but it is challenging to show a diagram with such a low degree. Therefore, I increased the angle to 10 degrees.